이항 인수분해 방법

작가: Janice Evans
창조 날짜: 28 칠월 2021
업데이트 날짜: 1 칠월 2024
Anonim
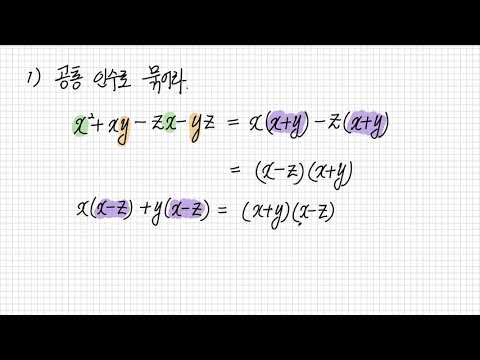
인수분해1
동영상: 인수분해1

콘텐츠

이항(이항)은 더하기 또는 빼기 기호가 있는 두 개의 항이 있는 수학적 표현입니다. 예를 들면 다음과 같습니다. NSNS+NS{ displaystyle ax + b}... 첫 번째 구성원은 변수를 포함하고 두 번째 구성원은 변수를 포함하거나 포함하지 않습니다. 이항식을 인수분해하는 것은 곱할 때 그것을 풀거나 단순화하기 위해 원래 이항식을 생성하는 항을 찾는 것을 포함합니다.

단계

파트 1/3: 이항 인수분해

  1. 1 인수분해 과정의 기초를 이해한다. 이항식을 인수분해할 때 원래 이항식의 각 항의 제수인 인수는 대괄호에서 제거됩니다. 예를 들어, 숫자 6은 1, 2, 3, 6으로 완전히 나눌 수 있습니다. 따라서 숫자 6의 제수는 숫자 1, 2, 3, 6입니다.
    • 제수 32: 1, 2, 4, 8, 16, 32.
    • 모든 숫자의 제수는 1과 숫자 자체입니다. 예를 들어, 3의 제수는 1과 3입니다.
    • 정수 제수는 정수만 될 수 있습니다. 숫자 32는 3.564 또는 21.4952로 나눌 수 있지만 정수가 아니라 소수를 얻습니다.
  2. 2 인수분해 과정을 용이하게 하기 위해 이항의 항을 정렬합니다. 이항은 두 항의 합 또는 차이며, 그 중 적어도 하나는 변수를 포함합니다. 때때로 변수는 다음과 같이 거듭제곱됩니다. NS2{ 디스플레이 스타일 x ^ {2}} 또는 5와이4{ 디스플레이 스타일 5년 ^ {4}}... 지수의 오름차순으로 이항식의 항을 정렬하는 것이 좋습니다. 즉, 지수가 가장 작은 항이 먼저 작성되고 가장 큰 항이 마지막에 기록됩니다. 예를 들어:
    • 3NS+6{ 디스플레이 스타일 3t + 6} → 6+3NS{ 디스플레이 스타일 6 + 3t}
    • 3NS4+9NS2{ 디스플레이 스타일 3x ^ {4} + 9x ^ {2}} → 9NS2+3NS4{ 디스플레이 스타일 9x ^ {2} + 3x ^ {4}}
    • NS2−2{ 표시 스타일 x ^ {2} -2} → −2+NS2{ 디스플레이 스타일 -2 + x ^ {2}}
      • 2 앞에 있는 빼기 기호에 주목하세요. 항을 빼면 그 앞에 빼기 기호를 씁니다.
  3. 3 두 항의 최대공약수(GCD)를 구합니다. GCD는 이항의 두 구성원을 나눌 수 있는 가장 큰 수입니다. 이렇게 하려면 이항에서 각 항의 제수를 찾은 다음 최대 공약수를 선택합니다. 예를 들어:
    • 작업:3NS+6{ 디스플레이 스타일 3t + 6}.
      • 제수 3: 1, 3
      • 제수 6: 1, 2, 3, 6.
      • GCD = 3.
  4. 4 이항식의 각 항을 최대공약수(GCD)로 나눕니다. 이 작업을 수행하여 GCD를 제외합니다. 이항식의 각 구성원은 감소하지만(나누기 때문에) GCD가 괄호에서 제외되면 최종 표현식은 원래 표현식과 같습니다.
    • 작업:3NS+6{ 디스플레이 스타일 3t + 6}.
    • GCD 찾기: 3
    • 각 이항 항을 gcd로 나눕니다.3NS3+63=NS+2{ displaystyle { frac {3t} {3}} + { frac {6} {3}} = t + 2}
  5. 5 제수를 괄호 밖으로 옮깁니다. 이전에 이항의 두 항을 제수 3으로 나누고 다음을 얻었습니다. NS+2{ 디스플레이 스타일 t + 2}... 그러나 3을 없앨 수는 없습니다. 초기 표현식과 최종 표현식의 값이 같게 하려면 괄호 밖에 3을 넣고 나눗셈의 결과로 얻은 표현식을 괄호 안에 써야 합니다. 예를 들어:
    • 작업:3NS+6{ 디스플레이 스타일 3t + 6}.
    • GCD 찾기: 3
    • 각 이항 항을 gcd로 나눕니다.3NS3+63=NS+2{ displaystyle { frac {3t} {3}} + { frac {6} {3}} = t + 2}
    • 결과 식에 제수를 곱합니다.3(NS+2){ 디스플레이 스타일 3(t + 2)}
    • 답변: 3(NS+2){ 디스플레이 스타일 3(t + 2)}
  6. 6 답을 확인하세요. 이렇게 하려면 대괄호 앞의 항에 대괄호 안의 각 항을 곱하십시오. 원래 이항식을 얻으면 솔루션이 정확합니다. 이제 문제를 해결 12NS+18{ 디스플레이 스타일 12t + 18}:
    • 회원 주문:18+12NS{ 디스플레이 스타일 18 + 12t}
    • GCD 찾기:6{ 디스플레이 스타일 6}
    • 각 이항 항을 gcd로 나눕니다.18NS6+12NS6=3+2NS{ displaystyle { frac {18t} {6}} + { frac {12t} {6}} = 3 + 2t}
    • 결과 표현식으로 제수를 곱합니다.6(3+2NS){ 디스플레이 스타일 6 (3 + 2t)}
    • 답을 확인하십시오.(6∗3)+(6∗2NS)=18+12NS{ 표시 스타일 (6 * 3) + (6 * 2t) = 18 + 12t}

3/2부: 방정식 풀이를 위한 이항 인수분해

  1. 1 이항식을 인수분해하여 단순화하고 방정식을 풉니다. 언뜻 보기에 일부 방정식(특히 복소수 이항식)을 푸는 것이 불가능해 보입니다. 예를 들어 방정식을 풉니다. 5와이−2와이2=−3와이{ 디스플레이 스타일 5년-2년 ^ {2} = - 3년}... 이 방정식에는 거듭제곱이 있으므로 먼저 식을 인수분해하십시오.
    • 작업:5와이−2와이2=−3와이{ 디스플레이 스타일 5년-2년 ^ {2} = - 3년}
    • 이항식에는 두 개의 구성원이 있음을 기억하십시오. 표현식에 더 많은 항이 포함된 경우 다항식을 푸는 방법을 배웁니다.
  2. 2 방정식의 한쪽에 0이 남도록 방정식의 양쪽에 일부 단항식을 더하거나 뺍니다. 인수분해의 경우 방정식에 대한 솔루션은 0을 곱한 모든 표현식이 0과 같다는 불변의 사실을 기반으로 합니다. 따라서 방정식을 0과 동일시하면 해당 요인 중 하나라도 0과 같아야 합니다. 방정식의 한 변을 0으로 설정합니다.
    • 작업:5와이−2와이2=−3와이{ 디스플레이 스타일 5년-2년 ^ {2} = - 3년}
    • 0으로 설정:5와이−2와이2+3와이=−3와이+3와이{ 디스플레이 스타일 5년-2년 ^ {2} + 3년 = -3년 + 3년}
      • 8와이−2와이2=0{ 디스플레이 스타일 8년-2년 ^ {2} = 0}
  3. 3 결과 빈을 인수분해합니다. 이전 섹션에서 설명한 대로 이 작업을 수행합니다. 최대공약수(GCD)를 찾아 이항의 두 항을 나눈 다음, 인수를 괄호 밖으로 옮깁니다.
    • 작업:5와이−2와이2=−3와이{ 디스플레이 스타일 5년-2년 ^ {2} = - 3년}
    • 0으로 설정:8와이−2와이2=0{ 디스플레이 스타일 8년-2년 ^ {2} = 0}
    • 요인:2와이(4−와이)=0{ 디스플레이 스타일 2년(4년) = 0}
  4. 4 각 요소를 0으로 설정합니다. 결과 표현식에서 2y는 4 - y를 곱하고 이 곱은 0과 같습니다. 0을 곱한 표현식(또는 항)은 0이므로 2y 또는 4 - y는 0입니다. 결과 단항 및 이항을 0으로 설정하여 "y"를 찾습니다.
    • 작업:5와이−2와이2=−3와이{ 디스플레이 스타일 5년-2년 ^ {2} = - 3년}
    • 0으로 설정:8와이−2와이2+3와이=0{ 디스플레이 스타일 8년-2년 ^ {2} + 3년 = 0}
    • 요인:2와이(4−와이)=0{ 디스플레이 스타일 2년(4년) = 0}
    • 두 요소를 모두 0으로 설정합니다.
      • 2와이=0{ 디스플레이 스타일 2y = 0}
      • 4−와이=0{ 디스플레이 스타일 4-y = 0}
  5. 5 최종 답을 찾기 위해 결과 방정식을 푸십시오. 각 요인은 0과 같기 때문에 방정식은 여러 해를 가질 수 있습니다. 우리의 예에서:
    • 2와이=0{ 디스플레이 스타일 2y = 0}
      • 2와이2=02{ displaystyle { frac {2y} {2}} = { frac {0} {2}}}
      • y = 0
    • 4−와이=0{ 디스플레이 스타일 4-y = 0}
      • 4−와이+와이=0+와이{ 디스플레이 스타일 4-y + y = 0 + y}
      • y = 4
  6. 6 답을 확인하세요. 이렇게하려면 찾은 값을 원래 방정식에 대입하십시오. 평등이 참이면 결정이 옳습니다. "y"대신 찾은 값을 대체하십시오. 이 예에서 y = 0 및 y = 4:
    • 5(0)−2(0)2=−3(0){ 디스플레이 스타일 5(0) -2(0) ^ {2} = - 3(0)}
      • 0+0=0{ 디스플레이 스타일 0 + 0 = 0}
      • 0=0{ 디스플레이 스타일 0 = 0}이것은 올바른 결정입니다
    • 5(4)−2(4)2=−3(4){ 디스플레이 스타일 5(4) -2(4) ^ {2} = - 3(4)}
      • 20−32=−12{ 디스플레이 스타일 20-32 = -12}
      • −12=−12{ 디스플레이 스타일 -12 = -12}그리고 이것은 올바른 결정입니다

3/3부: 복잡한 문제 해결

  1. 1 변수가 거듭제곱된 경우에도 변수가 있는 항은 인수분해될 수 있음을 기억하십시오. 인수 분해할 때 이항의 각 구성원을 통합적으로 나누는 단항을 찾아야 합니다. 예를 들어, 단항 NS4{ 디스플레이 스타일 x ^ {4}} 인수분해될 수 있다 NS∗NS∗NS∗NS{ 디스플레이 스타일 x * x * x * x}... 즉, 이항식의 두 번째 항에 변수 "x"도 포함되어 있으면 대괄호에서 "x"를 빼낼 수 있습니다. 따라서 변수를 정수로 취급하십시오. 예를 들어:
    • 이항의 두 구성원 2NS+NS2{ 디스플레이 스타일 2t + t ^ {2}} "t"를 포함하므로 "t"를 괄호에서 빼낼 수 있습니다. NS(2+NS){ 디스플레이 스타일 t (2 + t)}
    • 또한, 거듭제곱한 변수는 대괄호에서 꺼낼 수 있습니다. 예를 들어, 이항의 두 구성원 NS2+NS4{ 디스플레이 스타일 x ^ {2} + x ^ {4}} 포함하다 NS2{ 디스플레이 스타일 x ^ {2}}, 그래서 NS2{ 디스플레이 스타일 x ^ {2}} 브래킷에서 꺼낼 수 있습니다. NS2(1+NS2){ displaystyle x ^ {2} (1 + x ^ {2})}
  2. 2 이항식을 얻으려면 유사한 항을 더하거나 빼십시오. 예를 들어 표현식이 주어졌을 때 6+2NS+14+3NS{ 디스플레이 스타일 6 + 2x + 14 + 3x}... 언뜻 보기에는 다항식이지만 실제로는 이 표현식을 이항식으로 변환할 수 있습니다. 유사한 용어 추가: 6 및 14(변수를 포함하지 않음), 2x 및 3x(동일한 변수 "x" 포함). 이 경우 인수분해 프로세스가 단순화됩니다.
    • 원래 표현:6+2NS+14+3NS{ 디스플레이 스타일 6 + 2x + 14 + 3x}
    • 회원 주문:2NS+3NS+14+6{ 디스플레이 스타일 2x + 3x + 14 + 6}
    • 유사한 용어 추가:5NS+20{ 디스플레이 스타일 5x + 20}
    • GCD 찾기:5(NS)+5(4){ 디스플레이 스타일 5(x) +5(4)}
    • 요인:5(NS+4){ 디스플레이 스타일 5(x + 4)}
  3. 3 완전제곱수의 차를 인수분해합니다. 완전제곱수는 제곱근이 정수인 숫자입니다. 예를 들어 9{ 디스플레이 스타일 9}(3∗3){ 표시 스타일 (3 * 3)}, NS2{ 디스플레이 스타일 x ^ {2}}(NS∗NS){ 표시 스타일 (x * x)} 그리고 심지어 144NS2{ 디스플레이 스타일 144t ^ {2}}(12NS∗12NS){ 디스플레이 스타일 (12t * 12t)}... 예를 들어, 이항이 완전제곱수의 차라면, NS2−NS2{ displaystyle a ^ {2} -b ^ {2}}, 다음 공식으로 인수분해됩니다.
    • 제곱식의 차이:NS2−NS2=(NS+NS)(NS−NS){ displaystyle a ^ {2} -b ^ {2} = (a + b) (a-b)}
    • 작업:4NS2−9{ displaystyle 4x ^ {2} -9}
    • 제곱근을 추출합니다.
      • 4NS2=2NS{ displaystyle { sqrt {4x ^ {2}}} = 2x}
      • 9=3{ displaystyle { sqrt {9}} = 3}
    • 찾은 값을 공식에 ​​대입합니다. 4NS2−9=(2NS+3)(2NS−3){ displaystyle 4x ^ {2} -9 = (2x + 3) (2x-3)}
  4. 4 완전한 큐브 간의 차이를 고려하십시오. 예를 들어, 이항이 완전한 큐브의 차이인 경우, NS3−NS3{ displaystyle a ^ {3} -b ^ {3}}, 그런 다음 특수 공식을 사용하여 인수분해됩니다. 이 경우 이항식의 각 구성원에서 세제곱근을 추출하고 찾은 값을 수식에 대입해야 합니다.
    • 큐브의 차이에 대한 공식:NS3−NS3=(NS−NS)(NS2+NSNS+NS2){ displaystyle a ^ {3} -b ^ {3} = (a-b) (a ^ {2} + ab + b ^ {2})}
    • 작업:8NS3−27{ displaystyle 8x ^ {3} -27}
    • 입방근 추출:
      • 8NS33=2NS{ displaystyle { sqrt [{3}] {8x ^ {3}}} = 2x}
      • 273=3{ displaystyle { sqrt [{3}] {27}} = 3}
    • 찾은 값을 공식에 ​​대입합니다. 8NS3−27=(2NS−3)(4NS2+6NS+9){ displaystyle 8x ^ {3} -27 = (2x-3) (4x ^ {2} + 6x + 9)}
  5. 5 전체 큐브의 합을 인수분해합니다. 예를 들어, 완전제곱합의 합과 달리 완전한 입방체의 합은 다음과 같습니다. NS3+NS3{ displaystyle a ^ {3} + b ^ {3}}, 특수 공식을 사용하여 인수분해할 수 있습니다. 정육면체의 차이에 대한 공식과 유사하지만 부호가 반대입니다. 공식은 매우 간단합니다. 사용하려면 문제에서 전체 큐브의 합을 찾으십시오.
    • 큐브 합계 공식:NS3+NS3=(NS+NS)(NS2−NSNS+NS2){ displaystyle a ^ {3} + b ^ {3} = (a + b) (a ^ {2} -ab + b ^ {2})}
    • 작업:8NS3−27{ displaystyle 8x ^ {3} -27}
    • 입방근 추출:
      • 8NS33=2NS{ displaystyle { sqrt [{3}] {8x ^ {3}}} = 2x}
      • 273=3{ displaystyle { sqrt [{3}] {27}} = 3}
    • 찾은 값을 공식에 ​​대입합니다. 8NS3−27=(2NS+3)(4NS2−6NS+9){ displaystyle 8x ^ {3} -27 = (2x + 3) (4x ^ {2} -6x + 9)}

팁

  • 때때로 이항 구성원은 공약수가 없습니다. 일부 작업에서는 구성원이 단순화된 형식으로 표시됩니다.
  • GCD를 바로 찾을 수 없으면 작은 숫자로 나누어 시작하십시오. 예를 들어, 숫자 32와 16의 GCD가 16이라는 것을 알 수 없으면 두 숫자를 모두 2로 나눕니다. 16과 8을 얻습니다. 이 숫자는 8로 나눌 수 있습니다. 이제 2와 1을 얻습니다. 이 숫자는 줄일 수 없습니다. 따라서 주어진 두 수의 공약수인 더 큰 수(8 및 2에 비해)가 있음이 분명합니다.
  • 6차 항(예: x의 지수가 6인 항)은 완전 제곱과 완전 세제곱입니다. 따라서 예를 들어 x - 64와 같은 6차 항을 갖는 이항식에 제곱의 차이와 세제곱의 차이에 대한 공식을 (순서에 관계없이) 적용할 수 있습니다. 그러나 이항으로 더 정확하게 분해하려면 먼저 제곱의 차에 대한 공식을 적용하는 것이 좋습니다.

경고

  • 완전제곱수의 합인 이항은 인수분해할 수 없습니다.

당신에게 추천합니다

YouTube에서 구독자를 보는 방법
YouTube에서 구독자를 보는 방법
차 멀미에 대처하는 방법
차 멀미에 대처하는 방법
여자 친구가 혼자 시간을 보내고 싶어하게 만드는 방법
여자 친구가 혼자 시간을 보내고 싶어하게 만드는 방법
곡물 딱정벌레를 죽이는 방법
곡물 딱정벌레를 죽이는 방법