콘텐츠

• 단계
• 팁

유리 함수의 형식은 y = N(x) / D(x)이며, 여기서 N과 D는 다항식입니다. 이러한 함수를 정확하게 플로팅하려면 미분 계산을 포함하여 대수학에 대한 좋은 지식이 필요합니다. 다음 예를 고려하십시오. 와이 = (2NS - 6NS + 5)/(4NS + 2).

단계

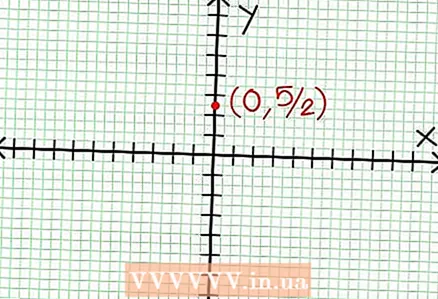1. 1 그래프의 y절편을 찾습니다. 이렇게 하려면 함수에 x = 0을 대입하고 y = 5/2를 얻습니다. 따라서 그래프와 Y축의 교차점은 좌표(0, 5/2)를 갖습니다.이 점을 좌표 평면에 배치합니다.
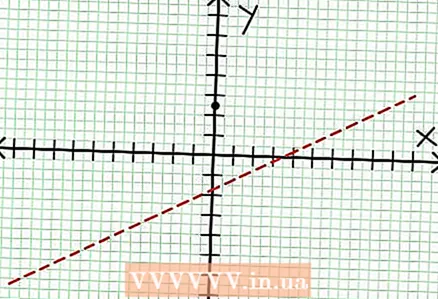2. 2 수평 점근선을 찾습니다. 분자를 분모(열에서)로 나누어 "x" 값이 무한대로 향하는 "y" 동작을 결정합니다. 이 예에서 나눗셈은 와이 = (1/2)NS - (7/4) + 17/(8NS + 4). "x"의 큰 양수 또는 음수 값의 경우 17 / (8NS + 4) 0에 가까워지고 그래프가 함수에 의해 주어진 직선에 접근합니다. 와이 = (1/2)NS - (7/4). 점선을 사용하여 이 함수를 플로팅합니다.
   • 분자의 차수가 분모의 차수보다 작으면 분자를 분모로 나눌 수 없으며 점근선은 함수로 설명됩니다. ~에 = 0.
   • 분자의 차수가 분모의 차수와 같으면 점근선은 가장 높은 차수의 "x"에 있는 계수의 비율과 같은 수평선입니다.
   • 분자의 차수가 분모의 차수보다 1 더 크면 점근선은 경사진 직선이며 그 기울기는 "x"에서 가장 높은 차수에 대한 계수의 비율과 같습니다.
   • 분자의 차수가 분모의 차수보다 2, 3 등으로 큰 경우 큰 값의 경우 |NS| 의미 ~에 제곱, 입방 또는 기타 다항식의 형태로 무한대(양수 또는 음수)가 되는 경향이 있습니다. 이 경우 분자를 분모로 나누어 얻은 함수의 정확한 그래프를 작성할 필요가 없을 가능성이 큽니다.
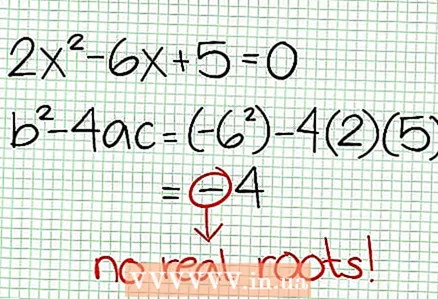3. 3 함수의 0을 찾습니다. 유리수 함수는 분자가 0일 때, 즉 N(NS) = 0. 이 예에서는 2NS - 6NS + 5 = 0. 이 2차 방정식의 판별식: NS - 4교류 = 6 - 4 * 2 * 5 = 36 - 40 = -4. 판별식이 음수이므로 N(NS), 따라서 F(NS)에는 실제 뿌리가 없습니다. 유리수 함수의 그래프는 X축과 교차하지 않으며, 함수에 0(근)이 있으면 좌표 평면에 놓습니다.
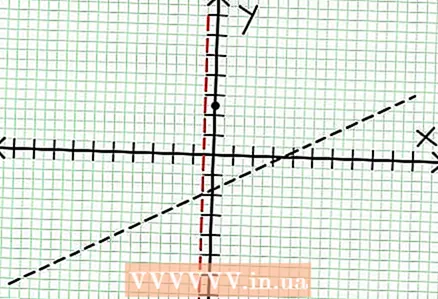4. 4 수직 점근선을 찾습니다. 이렇게 하려면 분모를 0으로 설정합니다. 이 예에서는 4NS + 2 = 0 및 NS = -1/2. 점선을 사용하여 수직 점근선을 플로팅합니다. 어떤 가치를 위해 NS NS (NS) = 0 및 D(NS) = 0이면 수직 점근선이 존재하거나 존재하지 않습니다(드문 경우이지만 기억하는 것이 좋습니다).
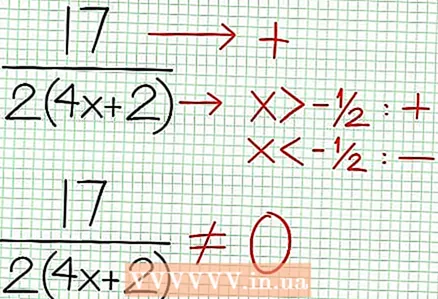5. 5 분자를 분모로 나눈 나머지를 보십시오. 양수입니까, 음수입니까, 아니면 0입니까? 이 예에서 나머지는 17이며 양수입니다. 분모 4NS + 2 수직 점근선의 오른쪽에 양수이고 왼쪽에 음수입니다. 이것은 큰 양수 값에 대한 유리 함수의 그래프가 NS 위에서부터 점근선에 접근하고 큰 음수 값에 대해 NS - 밑에서부터. 17 / (8NS + 4) 가 0과 같지 않으면 이 함수의 그래프는 함수에서 지정한 직선과 절대 교차하지 않습니다. ~에 = (1/2)NS - (7/4).
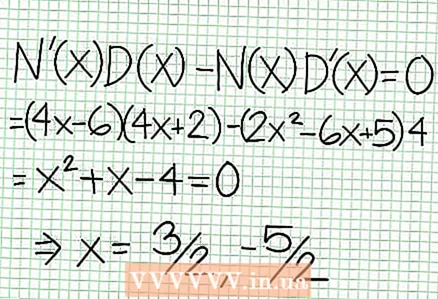6. 6 극한값을 구합니다. N '(NS) NS (NS) - NS (NS) NS '(NS) = 0. 이 예에서 N '(NS) = 4NS - 6 및 D'(NS) = 4. N '(NS) NS (NS) - NS (NS) NS '(NS) = (4NS - 6)(4NS + 2) - (2NS - 6NS + 5)*4 = NS + NS - 4 = 0. 이 방정식을 풀면 NS = 3/2 및 NS = -5/2. (완전히 정확한 값은 아니지만 초정밀이 필요하지 않은 경우에 적합합니다.)
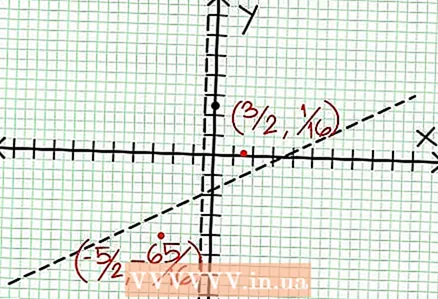7. 7 가치 찾기 ~에 각 극한값에 대해. 이렇게 하려면 값을 대체하십시오. NS 원래 합리적 기능으로. 이 예에서 f(3/2) = 1/16 및 f(-5/2) = -65/16입니다. 좌표 평면에서 점(3/2, 1/16) 및 (-5/2, -65/16)을 따로 설정합니다. 계산은 대략적인 값(이전 단계에서)을 기반으로 하기 때문에 발견된 최소값과 최대값도 완전히 정확하지 않습니다(그러나 정확한 값에 매우 가깝습니다). (점(3/2, 1/16)은 극소값에 매우 가깝습니다. 3단계부터 ~에 항상 긍정적인 NS> -1/2이고 작은 값(1/16)을 찾았습니다. 따라서 이 경우 오류 값은 매우 작습니다.)
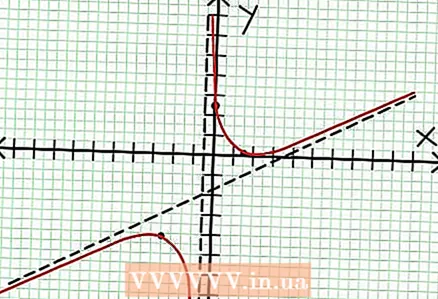8. 8 보류 점을 연결하고 그래프를 점근선으로 부드럽게 확장합니다(그래프가 점근선에 접근하는 올바른 방향을 잊지 마십시오). 그래프가 X축을 가로지르면 안 된다는 점을 기억하십시오(3단계 참조). 그래프는 또한 수평 및 수직 점근선과 교차하지 않습니다(5단계 참조). 이전 단계에서 찾은 극점을 제외하고 차트의 방향을 변경하지 마십시오.

팁

• 위의 단계를 순서대로 엄격히 따랐다면 솔루션을 테스트하기 위해 2차 도함수(또는 유사한 복소수)를 계산할 필요가 없습니다.
• 수량 값을 계산할 필요가 없는 경우 추가 좌표 쌍(NS, ~에) 각 점근선 쌍 사이. 또한 설명 된 방법이 어떻게 작동하는지 신경 쓰지 않는다면 왜 도함수를 찾지 못하고 방정식 N '(NS) NS (NS) - NS (NS) NS '(NS) = 0.
• 어떤 경우에는 고차 다항식으로 작업해야 합니다. 인수분해, 공식 등을 사용하여 정확한 해를 찾을 수 없으면 뉴턴 방법과 같은 수치적 방법을 사용하여 가능한 해를 추정합니다.
• 드문 경우지만 분자와 분모는 공통 변수 요소를 공유합니다. 설명된 단계에 따르면 이는 동일한 위치에서 0과 수직 점근선으로 이어집니다. 그러나 이는 불가능하며, 그 설명은 다음 중 하나입니다.
  • N의 0(NS)는 D(NS). 그래프 F(NS) 이 시점에서 0이 되는 경향이 있지만 거기에서 정의되지 않습니다. 점 주위에 원을 그려 이를 나타냅니다.
  • N의 0(NS) 및 D의 0(NS) 같은 다중성을 갖는다. 그래프는 이 값에서 0이 아닌 점에 접근합니다. NS그러나 거기에 정의되어 있지 않습니다. 점 주위에 원을 그려 이를 나타냅니다.
  • N의 0(NS)는 D(NS). 여기에 수직 점근선이 있습니다.